Tolerance interval

A tolerance interval is a statistical interval within which, with some confidence level, a specified proportion of a population falls.

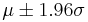A tolerance interval can be seen as a statistical version of a probability interval. If we knew a population's exact parameters, we would be able to compute a range within which a certain proportion of the population falls. For example, if we know a population is normally distributed with mean $\mu$ and standard deviation $\sigma$ , then the interval $\mu \pm 1.96\sigma$ includes 95% of the population (1.96 is the z-score for 95% coverage of a normally distributed population).

However, if we have only a sample from the population, we know only the sample mean 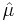$\hat{\mu}$ and sample standard deviation 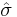$\hat{\sigma}$ , which are only estimates of the true parameters. In that case, 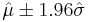$\hat{\mu} \pm 1.96\hat{\sigma}$ will not necessarily include 95% of the population, due to variance in these estimates. A tolerance interval bounds this variance by introducing a confidence level $\gamma$ , which is the confidence with which this interval actually includes the specified proportion of the population. For a normally distributed population, a z-score can be transformed into a "k factor" for a given $\gamma$ via lookup tables or several approximation formulas.^[1]

Relation to other intervals

The tolerance interval is less widely known than the confidence interval and prediction interval, a situation some educators have lamented, as it can lead to misuse of the other intervals where a tolerance interval is more appropriate.^[2]^[3]

The tolerance interval differs from a confidence interval in that the confidence interval bounds a single-valued population parameter (the mean or the variance, for example) with some confidence, while the tolerance interval bounds the range of data values that includes a specific proportion of the population. Whereas a confidence interval's size is entirely due to sampling error, and will approach a zero-width interval at the true population parameter as sample size increases, a tolerance interval's size is due partly to sampling error and partly to actual variance in the population, and will approach the population's probability interval as sample size increases.^[2]^[3]

The tolerance interval is related to a prediction interval in that both put bounds on variation in future samples. The prediction interval only bounds a single future sample, however, whereas a tolerance interval bounds the entire population (equivalently, an arbitrary sequence of future samples). In other words, a prediction interval covers a specified proportion of a population on average, whereas a tolerance interval covers it with a certain confidence level, making the tolerance interval more appropriate if a single interval is intended to bound multiple future samples.^[4]^[3]

Examples

^[2] gives the following example:

So consider once again a proverbial EPA mileage test scenario, in which several nominally identical autos of a particular model are tested to produce mileage figures $y_1, y_2, ..., y_n$ . If such data are processed to produce a 95% confidence interval for the mean mileage of the model, it is, for example, possible to use it to project the mean or total gasoline consumption for the manufactured fleet of such autos over their first 5,000 miles of use. Such an interval, would however, not be of much help to a person renting one of these cars and wondering whether the (full) 10-gallon tank of gas will suffice to carry him the 350 miles to his destination. For that job, a prediction interval would be much more useful. (Consider the differing implications of being "95% sure" that $\mu \ge 35$ as opposed to being "95% sure" that $y_{n%2B1} \ge 35$ .) But neither a confidence interval for $\mu$ nor a prediction interval for a single additional mileage is exactly what is needed by a design engineer charged with determining how large a gas tank the model really needs to guarantee that 99% of the autos produced will have a 400-mile cruising range. What the engineer really needs is a tolerance interval for a fraction $p = .99$ of mileages of such autos.

References

^ "Tolerance intervals for a normal distribution". Engineering Statistics Handbook. NIST/Sematech. 2010. http://www.itl.nist.gov/div898/handbook/prc/section2/prc263.htm. Retrieved 2011-08-26.
^ ^a ^b ^c Stephen B. Vardeman (1992). "What about the Other Intervals?". The American Statistician 46 (3): 193–197. JSTOR 2685212.
^ ^a ^b ^c Mark J. Nelson (2011-08-14). "You might want a tolerance interval". http://www.kmjn.org/notes/tolerance_intervals.html. Retrieved 2011-08-26.
^ K. Krishnamoorthy and Thomas Mathew (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. John Wiley and Sons. pp. 1–6. ISBN 0470380268.